Predicting Premier League Matches

Using Neural Networks and gradient boosting to predict Football matches

Author

Thomas H. Simm

Overview

Introduction

Predicting results of English Premier League using random forests for the 2017 to 2021 seasons. I will predict whether a result is a win, loss or draw, and then simplify as a binary question- is it a win?

From an article about pundit versus gambling company Pinnacle vs. Mark Lawrenson we have a benchmark to aim for from the 2012 season: - Mark Lawrenson = 52.6% accuracy - Pinnacle traders = 55.3% accuracy - Random guess = 33.3% accuracy

Method

In this data there are various parameters that can be used. The most important step is to not use data about a current match as a predictor, but for a prediction to be based on stats from previous matches. (A couple of slight exceptions to this are below like who is playing who and where)

The predictors used here include: - date of match - home or away - stats from previous matches - results - goals scored/conceded - possession/expected goals etc - who is playing who

Some details on the machine learning:

  • Notebook on kaggle is here
  • Several models were used:
  • Regression and classification models were used
  • Data is trained on years 2017 to 2020 with season 2021 used as validation
    • 20% validation / 80% training
  • Some data cleaning methods were performed and shown in the code

Results

  • Model accuracy = 52% (+-1%)

    • So the model is comparable with the results of Mark Lawrenson

  • The model is okay as it matches the accuracy from an expert pundit. But it does underperform gambing predictions.

  • Draws are under-represented by the model

    • draws predicted was increased by adjusting the input parameter class_weight but the issue was only reduced

  • Changing input parameters was done in a semi-manual manner, obtaining the best input parameters was not easy

  • The more parameters the better,

    • but the increase from just using a basic four parameter fit to one with 300+ columns is relatively small (a difference of ~1-2% (based on values 50-65%))

  • By searching for the best hyper parameters the results of a random forest (RF) model were increased from 49% accuracy to 52%

  • RF, XG boost and grad boost methods all performed similar

    • Ridge model was the worst performing
    • Neural networks with fastai tabular data also performed poorly. NN analysis of EPL

  • Similar results were obtained by using classification and regression methods

    • Regression on the net score performed the best
    • Regression methods performed worse on predicting draws though

  • Ensembling (combining results from different methods by adding them) can increase the overall results. The accuracy would need to be comparable and the results different enough for their to be a benefit

A summary of the results is shown below

Accuracy W/L/D Accuracy Win Classification/Regression Details
0.489 0.669 Classification RF with all parameters
0.479 0.661 Classification RF with 43 parameters from feature imp
0.487 0.666 Classification RF as above with basic features
0.484 0.656 Classification RF with 4 basic features
0.479 - Classification RF with 4 basic ones + balanced
0.485 0.656 Classification RF with 23 correlation parameters plus basic
0.451 0.678 Regression RF with all parameters on net score
- 0.657 Regression XGB with all parameters on net score
- 0.639 Regression Ridge with all parameters on net score
- 0.666 Regression Grad boost with all parameters on net score
0.427 0.670 Regression RF with all parameters on GF/GA
- 0.670 Regression XGB with all parameters on GF/GA score
- 0.665 Regression RF+XGB+Grad boost on netscore
- 0.678 Regression RF on netscore + RF on GF/GA

This notebook

In this notebook I’ll look at gradient boosting and neural networks. And then combine the results using Ensembling. i.e. the results of two different models predictions should be better than each individual one.

The binary version and more details on the models is found here

Code- Prepare the data

Data is prepared in a separate page- Predicting Premier League Matches- Prepare the data

Load data and libraries

#collapse-hide
import pandas as pd
import os
import numpy as np
import matplotlib.pyplot as plt
import copy

from sklearn.metrics import accuracy_score
from sklearn.metrics import mean_absolute_error

from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.compose import make_column_transformer

from sklearn.ensemble import RandomForestClassifier
from tensorflow import keras
from tensorflow.keras import layers, callbacks

# from sklearn.tree import DecisionTreeClassifier
# from dtreeviz.trees import *
# from pandas.api.types import is_string_dtype, is_numeric_dtype, is_categorical_dtype
# from fastai.tabular.all import *

# from sklearn.experimental import enable_halving_search_cv  # noqa
# from sklearn.model_selection import HalvingRandomSearchCV


# from sklearn.metrics import precision_score
from xgboost import XGBClassifier

cwd=os.getcwd()
folda=cwd+"/data/epl/"
dira = os.listdir(folda)
#collapse-output

dfAll=pd.read_csv(folda+'epl2017-2021_wivnetscoreAndGFGA_both-HA_modPC.csv',index_col=0)
dfAll=dfAll.iloc[20:,:]
dfAll
round day venue_x result_x gf_x ga_x opponent_x shooting_gls_x shooting_sh__x shooting_sot_x ... misc_int__y misc_tklw__y misc_pkwon_y misc_pkcon_y misc_og_y misc_recov_y misc_won_y misc_lost_y misc_won%_y team_y
44 3 27 Home 0.000000 2.000000 2.000000 Everton 2.000000 14.500000 4.000000 ... 13.000000 12.000000 0.000000 0.000000 0.000000 94.500000 19.500000 27.000000 41.150000 Everton
45 3 27 Away 0.000000 2.000000 2.000000 Liverpool 2.000000 23.000000 8.500000 ... 16.000000 12.000000 0.500000 0.000000 0.000000 114.000000 28.500000 20.500000 57.450000 Liverpool
46 3 27 Away 0.000000 1.500000 1.500000 Tottenham Hotspur 1.500000 15.000000 3.000000 ... 8.500000 9.000000 0.000000 0.000000 0.000000 91.000000 21.000000 22.500000 48.600000 Tottenham Hotspur
47 3 27 Away 0.500000 1.000000 0.500000 Chelsea 1.000000 8.000000 3.000000 ... 7.000000 14.000000 0.000000 0.000000 0.500000 92.000000 23.500000 26.000000 47.850000 Chelsea
48 3 26 Away 0.500000 2.500000 2.000000 Manchester United 2.500000 10.000000 3.500000 ... 16.000000 10.500000 0.000000 0.000000 0.000000 91.000000 21.500000 19.500000 50.300000 Manchester United
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
3795 38 22 Away 0.333333 1.666667 1.333333 Arsenal 1.666667 9.333333 4.000000 ... 10.000000 9.666667 0.000000 0.000000 0.333333 74.333333 14.666667 16.666667 46.466667 Arsenal
3796 38 22 Away -1.666667 0.666667 2.333333 Brentford 0.666667 9.666667 2.333333 ... 11.666667 6.666667 0.000000 0.666667 0.000000 80.333333 15.333333 15.666667 48.333333 Brentford
3797 38 22 Home -0.666667 1.000000 1.666667 Newcastle United 1.000000 13.000000 4.333333 ... 14.666667 13.000000 0.000000 0.000000 0.000000 64.333333 20.000000 19.000000 48.766667 Newcastle United
3798 38 22 Away -2.000000 0.666667 2.666667 Chelsea 0.333333 10.666667 2.666667 ... 11.666667 11.666667 0.333333 0.000000 0.000000 88.000000 17.666667 13.666667 57.066667 Chelsea
3799 38 22 Home -2.000000 0.333333 2.333333 Tottenham Hotspur 0.333333 9.666667 2.333333 ... 12.000000 9.666667 0.000000 0.000000 0.000000 81.666667 23.666667 17.000000 57.633333 Tottenham Hotspur

3740 rows × 333 columns

#collapse-output
with pd.option_context("display.max_columns", None):
    display(dfAll.describe(include='all'))
round day venue_x result_x gf_x ga_x opponent_x shooting_gls_x shooting_sh__x shooting_sot_x shooting_sot%_x shooting_g/sh_x shooting_g/sot_x shooting_PC_dist_x shooting_fk__x shooting_pk_x shooting_pkatt__x shooting_xg_x shooting_npxg_x shooting_npxg/sh_x shooting_g-xg_x shooting_np:g-xg_x keeper_sota_x keeper_saves_x keeper_save%_x keeper_cs_x keeper_psxg_x keeper_psxg+/-_x keeper_pkatt__x keeper_pka_x keeper_pksv_x keeper_pkm_x keeper_cmp__x keeper_att__x keeper_cmp%__x keeper_att_.1_x keeper_thr_x keeper_launch%_x keeper_avglen_x keeper_att_.2_x keeper_launch%.1_x keeper_avglen.1_x keeper_opp_x keeper_stp_x keeper_stp%_x keeper_#opa_x keeper_avgdist_x passing_pass_complete_x passing_cmp%__x passing_PC_totdist__x passing_PC_prgdist__x passing_PC_cmp_.1_x passing_cmp%_.1_x passing_PC_cmp_.2_x passing_cmp%_.2_x passing_PC_cmp_.3_x passing_cmp%_.3_x passing_ast_x passing_xa_x passing_kp_x passing_PC_1/3__x passing_PC_ppa_x passing_PC_crspa_x passing_PC_prog__x passing_PC_types_live__x passing_PC_types_dead_x passing_PC_types_fk__x passing_PC_types_tb_x passing_PC_types_press__x passing_PC_types_sw_x passing_PC_types_crs__x passing_PC_types_ck_x passing_PC_types_in_x passing_PC_types_out_x passing_PC_types_str_x passing_PC_types_ground_x passing_PC_types_low_x passing_PC_types_high_x passing_PC_types_left_x passing_PC_types_right_x passing_PC_types_head_x passing_PC_types_ti_x passing_PC_types_other_x passing_PC_types_cmp__x passing_PC_types_off__x passing_PC_types_out.1_x passing_PC_types_int__x passing_PC_types_blocks__x shotcreate_sca_x shotcreate_passlive_x shotcreate_passdead_x shotcreate_drib_x shotcreate_sh_gca_x shotcreate_fld_gca_x shotcreate_def_x shotcreate_gca_x shotcreate_passlive.1_x shotcreate_passdead.1_x shotcreate_drib.1_x shotcreate_sh_gca.1_x shotcreate_fld_gca.1_x shotcreate_def.1_x tackle_tkl_x tackle_PC_tklw_defense_x tackle_PC_def 3rd_defense_x tackle_PC_mid 3rd_defense_x tackle_PC_att 3rd_defense_x tackle_PC_tkl_dribble_x tackle_dribble%_x tackle_dribllepast_x tackle_press_defense_x tackle_%_x tackle_PC_press_def3rd_x tackle_PC_press_mid3rd_x tackle_PC_press_att3rd_x tackle_blocks_defense_x tackle_PC_sh_defense_x tackle_PC_shsv_x tackle_PC_pass_x tackle_int_defense_x tackle_clr_x tackle_err_x possession_poss_x possession_touches_x possession_PC_def pen_x possession_PC_def 3rd__x possession_PC_mid 3rd__x possession_PC_att 3rd__x possession_PC_att pen_x possession_PC_live__x possession_dribblesucc__x possession_dribbleatt__x possession_dribblesucc%_x possession_dribblepast_x possession_megs_x possession_carries_x possession_totdist__x possession_PC_prgdist__x possession_PC_prog__x possession_PC_1/3__x possession_PC_cpa_x possession_PC_mis_x possession_PC_dis_x possession_targ_x possession_rec_x possession_rec%_x possession_prog_.1_x misc_crdy_x misc_crdr_x misc_2crdy_x misc_fls_x misc_fld__x misc_off__x misc_crs__x misc_int__x misc_tklw__x misc_pkwon_x misc_pkcon_x misc_og_x misc_recov_x misc_won_x misc_lost_x misc_won%_x team_x season month year weekday Win_x NetScore_x GoalsFor_x GoalsAgainst_x result_y gf_y ga_y opponent_y shooting_gls_y shooting_sh__y shooting_sot_y shooting_sot%_y shooting_g/sh_y shooting_g/sot_y shooting_PC_dist_y shooting_fk__y shooting_pk_y shooting_pkatt__y shooting_yg_y shooting_npxg_y shooting_npxg/sh_y shooting_g-xg_y shooting_np:g-xg_y keeper_sota_y keeper_saves_y keeper_save%_y keeper_cs_y keeper_psxg_y keeper_psxg+/-_y keeper_pkatt__y keeper_pka_y keeper_pksv_y keeper_pkm_y keeper_cmp__y keeper_att__y keeper_cmp%__y keeper_att_.1_y keeper_thr_y keeper_launch%_y keeper_avglen_y keeper_att_.2_y keeper_launch%.1_y keeper_avglen.1_y keeper_opp_y keeper_stp_y keeper_stp%_y keeper_#opa_y keeper_avgdist_y passing_pass_complete_y passing_cmp%__y passing_PC_totdist__y passing_PC_prgdist__y passing_PC_cmp_.1_y passing_cmp%_.1_y passing_PC_cmp_.2_y passing_cmp%_.2_y passing_PC_cmp_.3_y passing_cmp%_.3_y passing_ast_y passing_ya_y passing_kp_y passing_PC_1/3__y passing_PC_ppa_y passing_PC_crspa_y passing_PC_prog__y passing_PC_types_live__y passing_PC_types_dead_y passing_PC_types_fk__y passing_PC_types_tb_y passing_PC_types_press__y passing_PC_types_sw_y passing_PC_types_crs__y passing_PC_types_ck_y passing_PC_types_in_y passing_PC_types_out_y passing_PC_types_str_y passing_PC_types_ground_y passing_PC_types_low_y passing_PC_types_high_y passing_PC_types_left_y passing_PC_types_right_y passing_PC_types_head_y passing_PC_types_ti_y passing_PC_types_other_y passing_PC_types_cmp__y passing_PC_types_off__y passing_PC_types_out.1_y passing_PC_types_int__y passing_PC_types_blocks__y shotcreate_sca_y shotcreate_passlive_y shotcreate_passdead_y shotcreate_drib_y shotcreate_sh_gca_y shotcreate_fld_gca_y shotcreate_def_y shotcreate_gca_y shotcreate_passlive.1_y shotcreate_passdead.1_y shotcreate_drib.1_y shotcreate_sh_gca.1_y shotcreate_fld_gca.1_y shotcreate_def.1_y tackle_tkl_y tackle_PC_tklw_defense_y tackle_PC_def 3rd_defense_y tackle_PC_mid 3rd_defense_y tackle_PC_att 3rd_defense_y tackle_PC_tkl_dribble_y tackle_dribble%_y tackle_dribllepast_y tackle_press_defense_y tackle_%_y tackle_PC_press_def3rd_y tackle_PC_press_mid3rd_y tackle_PC_press_att3rd_y tackle_blocks_defense_y tackle_PC_sh_defense_y tackle_PC_shsv_y tackle_PC_pass_y tackle_int_defense_y tackle_clr_y tackle_err_y possession_poss_y possession_touches_y possession_PC_def pen_y possession_PC_def 3rd__y possession_PC_mid 3rd__y possession_PC_att 3rd__y possession_PC_att pen_y possession_PC_live__y possession_dribblesucc__y possession_dribbleatt__y possession_dribblesucc%_y possession_dribblepast_y possession_megs_y possession_carries_y possession_totdist__y possession_PC_prgdist__y possession_PC_prog__y possession_PC_1/3__y possession_PC_cpa_y possession_PC_mis_y possession_PC_dis_y possession_targ_y possession_rec_y possession_rec%_y possession_prog_.1_y misc_crdy_y misc_crdr_y misc_2crdy_y misc_fls_y misc_fld__y misc_off__y misc_crs__y misc_int__y misc_tklw__y misc_pkwon_y misc_pkcon_y misc_og_y misc_recov_y misc_won_y misc_lost_y misc_won%_y team_y
count 3740.000000 3740.000000 3740 3740.000000 3740.000000 3740.000000 3740 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740 3740.000000 3740.000000 3740.000000 3740.000000 3740 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740.000000 3740
unique NaN NaN 2 NaN NaN NaN 28 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 28 NaN NaN NaN NaN 3 NaN NaN NaN NaN NaN NaN 28 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 28
top NaN NaN Away NaN NaN NaN Newcastle United NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN Burnley NaN NaN NaN NaN L NaN NaN NaN NaN NaN NaN Burnley NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN Newcastle United
freq NaN NaN 1871 NaN NaN NaN 188 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 188 NaN NaN NaN NaN 1444 NaN NaN NaN NaN NaN NaN 188 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN 188
mean 19.789305 15.910160 NaN -0.003342 1.367870 1.371212 NaN 1.324242 12.318806 4.082620 33.666230 0.103205 0.295620 151.814870 0.457487 0.104055 0.131684 1.320134 1.220357 0.100935 0.004109 -0.000169 4.084715 2.817513 68.905134 0.285829 1.332852 0.005624 0.134447 0.104768 0.022103 0.007576 6.711765 17.383601 41.413993 24.147148 4.075178 51.061034 42.502959 7.459848 66.906448 52.437215 8.755080 0.661631 7.543382 0.649643 14.412273 390.931194 77.247553 1979.363069 687.824335 40.897515 86.660709 41.792130 83.940147 15.411750 57.009621 0.942959 0.897821 8.928030 7.547074 2.120160 0.545131 8.387274 89.802235 10.197765 2.484955 0.183265 15.459547 2.967840 2.486263 1.061565 0.467084 0.350791 0.082297 63.555635 14.102166 22.342199 27.469285 59.267074 4.388067 4.484950 1.347329 77.794521 0.354085 1.919054 2.424604 2.519446 19.230080 13.878342 1.687032 1.185428 0.992647 1.057353 0.429278 2.148217 1.469563 0.141355 0.147816 0.180793 0.159358 0.049332 17.782130 60.717652 50.005406 37.636636 12.357958 33.790802 36.547767 10.469430 150.873797 29.555771 34.517406 43.220499 22.262095 15.869519 23.681976 0.506995 76.318024 12.285829 25.121970 0.274911 49.998217 615.295811 11.131009 33.164347 46.679487 26.100825 3.856162 92.155582 9.629144 16.482531 58.265330 10.457442 0.714572 383.570811 1960.431774 53.252857 10.944362 3.339541 1.091207 3.437701 3.274796 465.705749 390.931194 82.527647 34.576738 1.634715 0.058289 0.023886 12.389394 11.971569 1.868182 12.004590 12.285829 10.759091 0.110116 0.128832 0.044251 90.116667 19.210250 19.209581 49.993079 NaN 2019.023529 6.763636 2019.533690 4.360963 NaN -0.001872 1.371390 1.373262 -0.001471 1.368672 1.370143 NaN 1.324777 12.322950 4.084759 33.665749 0.103174 0.295648 151.783431 0.457888 0.104189 0.131818 1.320963 1.221092 0.100949 0.003815 -0.000504 4.081640 2.815374 68.919652 0.286364 1.331836 0.005677 0.134447 0.104768 0.022103 0.007576 6.709358 17.376381 41.415183 24.147549 4.076114 51.039416 42.493012 7.457843 66.902732 52.430985 8.752540 0.662701 7.562781 0.649777 14.412968 391.065285 77.252794 1979.240478 687.729735 40.898842 86.663770 41.792418 83.941805 15.409745 57.018378 0.943093 0.898075 8.930303 7.547489 2.119949 0.544611 8.387497 89.804963 10.195037 2.483827 0.183429 15.457410 2.966877 2.485392 1.061554 0.466670 0.351048 0.082452 63.562637 14.102245 22.335118 27.463310 59.275168 4.386860 4.484425 1.347030 77.799389 0.353852 1.918207 2.423601 2.519481 19.238102 13.884492 1.687299 1.185963 0.993182 1.058021 0.429144 2.149020 1.470766 0.141087 0.147683 0.180526 0.159759 0.049198 17.784135 60.719894 50.000323 37.647136 12.352541 33.783894 36.543182 10.470232 150.897059 29.560998 34.512083 43.224267 22.263651 15.867112 23.665236 0.506995 76.334764 12.288636 25.107932 0.274777 50.007442 615.434180 11.127372 33.157686 46.683163 26.103830 3.856597 92.157298 9.633021 16.488681 58.268097 10.461988 0.714840 383.703164 1960.965196 53.255401 10.945468 3.339802 1.091572 3.436512 3.274502 465.841176 391.065285 82.532513 34.589305 1.635918 0.058422 0.024020 12.391800 11.971836 1.866979 12.004055 12.288636 10.760561 0.110250 0.128832 0.044251 90.128164 19.211854 19.208779 49.995499 NaN
std 10.812190 9.082985 NaN 1.260926 0.808001 0.774004 NaN 0.794644 3.597818 1.608375 9.614793 0.063311 0.160978 54.846307 0.401409 0.189608 0.213964 0.539431 0.499269 0.028063 0.548592 0.545514 1.536609 1.192484 17.268237 0.271639 0.620853 0.426968 0.218550 0.189411 0.089500 0.052022 2.673514 6.831725 11.779479 5.578168 1.668569 20.032654 9.608195 2.134183 24.745854 13.899819 2.799294 0.530528 6.377266 0.567336 3.132228 119.477131 6.127586 108.661242 122.423021 3.621674 3.653049 3.620413 5.360235 2.776097 8.948543 0.660216 0.400746 2.878542 1.266651 0.599713 0.297163 1.457260 2.574413 2.574413 0.758481 0.151459 3.983513 0.780574 0.691667 0.342776 0.294596 0.231719 0.116260 9.270781 2.990125 7.202335 6.437151 7.071222 1.538933 1.257358 0.410721 6.000126 0.218160 0.703913 0.971685 0.625166 6.158332 5.057429 0.842449 0.768469 0.696029 0.600697 0.406695 1.383549 1.122031 0.214337 0.251428 0.253063 0.238379 0.133121 3.479814 7.282239 9.782546 7.986327 5.688972 8.586122 8.484729 2.904268 27.877080 3.933526 6.492833 3.781661 5.400574 3.425881 8.158337 1.101893 8.158337 4.887549 7.802474 0.332278 9.573898 112.341294 3.073200 5.869180 4.246802 4.196696 0.939337 1.639189 2.899335 4.097558 8.885281 3.039749 0.565743 109.013451 560.207630 3.728944 1.931172 0.714923 0.444086 1.165160 1.051011 119.023950 119.477131 5.138379 10.830988 0.746549 0.138407 0.089291 2.524250 2.591855 0.956812 3.444791 4.887549 2.295753 0.195497 0.211274 0.118976 11.267654 5.659847 5.813950 6.294121 NaN 1.407382 3.969227 1.520015 1.798241 NaN 1.947079 1.269421 1.269820 1.262519 0.808628 0.774343 NaN 0.795351 3.597067 1.608762 9.614106 0.063220 0.160880 54.850292 0.401701 0.189711 0.214038 0.540175 0.499985 0.028062 0.548811 0.545793 1.537276 1.192771 17.264720 0.271814 0.621129 0.426749 0.218550 0.189411 0.089500 0.052022 2.672028 6.828191 11.780052 5.577480 1.669308 20.034401 9.606079 2.134818 24.737701 13.894690 2.800754 0.530705 6.392757 0.567242 3.129257 119.515735 6.128051 108.609872 122.401336 3.621302 3.653428 3.620178 5.359233 2.775348 8.950187 0.660886 0.400693 2.874659 1.266934 0.599507 0.297272 1.457096 2.574378 2.574378 0.758191 0.151427 3.984765 0.780327 0.691138 0.342928 0.294658 0.231838 0.116712 9.267060 2.989201 7.200972 6.427083 7.065863 1.538999 1.256937 0.410498 6.000922 0.218247 0.704214 0.971906 0.625276 6.153878 5.053910 0.842469 0.768861 0.697474 0.601022 0.406260 1.385009 1.123701 0.213889 0.251374 0.252460 0.238531 0.132919 3.477123 7.276880 9.780540 7.986417 5.689568 8.581289 8.469441 2.904276 27.861281 3.935946 6.495629 3.784094 5.401501 3.426921 8.160210 1.101893 8.160210 4.886419 7.791726 0.332288 9.576615 112.388551 3.076070 5.875037 4.250795 4.198132 0.939326 1.639047 2.902260 4.103303 8.886728 3.042843 0.565759 109.038437 560.266760 3.730208 1.932012 0.714515 0.443880 1.164719 1.050918 119.069075 119.515735 5.138246 10.836724 0.746286 0.138592 0.089629 2.523003 2.591213 0.956610 3.445064 4.886419 2.293386 0.195592 0.211274 0.118976 11.274286 5.658357 5.813577 6.295669 NaN
min 1.000000 1.000000 NaN -5.333333 0.000000 0.000000 NaN 0.000000 3.333333 0.333333 2.766667 0.000000 0.000000 55.061728 0.000000 0.000000 0.000000 0.200000 0.166667 0.033333 -1.966667 -1.700000 0.333333 0.000000 -25.000000 0.000000 0.000000 -1.833333 0.000000 0.000000 0.000000 0.000000 0.666667 2.333333 9.333333 10.000000 0.000000 7.933333 22.033333 1.000000 0.000000 10.733333 1.333333 0.000000 0.000000 0.000000 4.000000 157.000000 58.200000 1690.290290 421.044850 28.197674 68.133333 31.100478 63.566667 8.301527 32.133333 0.000000 0.100000 1.666667 3.724138 0.126263 0.000000 3.750000 78.957169 3.957997 0.732601 0.000000 5.770965 1.133948 0.632911 0.000000 0.000000 0.000000 0.000000 32.774674 6.373355 6.699548 12.052117 37.898687 1.231423 1.332795 0.264901 58.153846 0.000000 0.455581 0.293255 0.691017 4.666667 2.500000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 7.333333 36.170213 11.627907 12.500000 0.000000 8.333333 9.166667 2.000000 66.000000 13.700000 13.606911 29.111842 8.041237 6.000000 0.000000 0.000000 45.161290 1.333333 6.333333 0.000000 24.666667 361.666667 3.639121 14.908854 33.405172 10.754098 1.246334 85.822785 2.000000 5.000000 22.333333 3.000000 0.000000 157.000000 778.000000 41.276202 5.420561 1.097695 0.000000 0.894188 0.889193 219.333333 157.000000 61.866667 10.666667 0.000000 0.000000 0.000000 4.333333 3.666667 0.000000 3.000000 1.333333 4.333333 0.000000 0.000000 0.000000 50.333333 4.000000 5.666667 22.200000 NaN 2017.000000 1.000000 2017.000000 0.000000 NaN -9.000000 0.000000 0.000000 -5.333333 0.000000 0.000000 NaN 0.000000 3.333333 0.333333 2.766667 0.000000 0.000000 55.061728 0.000000 0.000000 0.000000 0.200000 0.166667 0.033333 -1.966667 -1.700000 0.333333 0.000000 -25.000000 0.000000 0.000000 -1.833333 0.000000 0.000000 0.000000 0.000000 0.666667 2.333333 9.333333 10.000000 0.000000 7.933333 22.033333 1.000000 0.000000 10.733333 1.333333 0.000000 0.000000 0.000000 4.000000 157.000000 58.200000 1690.290290 421.044850 28.197674 68.133333 31.100478 63.566667 8.301527 32.133333 0.000000 0.100000 1.666667 3.724138 0.126263 0.000000 3.750000 78.957169 3.957997 0.732601 0.000000 5.770965 1.133948 0.632911 0.000000 0.000000 0.000000 0.000000 32.774674 6.373355 6.699548 12.052117 37.898687 1.231423 1.332795 0.264901 58.153846 0.000000 0.455581 0.293255 0.691017 4.666667 2.500000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 7.333333 36.170213 11.627907 12.500000 0.000000 8.333333 9.166667 2.000000 66.000000 13.700000 13.606911 29.111842 8.041237 6.000000 0.000000 0.000000 45.161290 1.333333 6.333333 0.000000 24.666667 361.666667 3.639121 14.908854 33.405172 10.754098 1.246334 85.822785 2.000000 5.000000 22.333333 3.000000 0.000000 157.000000 778.000000 41.276202 5.420561 1.097695 0.000000 0.894188 0.889193 219.333333 157.000000 61.866667 10.666667 0.000000 0.000000 0.000000 4.333333 3.666667 0.000000 3.000000 1.333333 4.333333 0.000000 0.000000 0.000000 50.333333 4.000000 5.666667 22.200000 NaN
25% 10.000000 8.000000 NaN -1.000000 0.666667 0.666667 NaN 0.666667 9.666667 3.000000 27.200000 0.060000 0.176667 114.758929 0.000000 0.000000 0.000000 0.933333 0.866667 0.080000 -0.366667 -0.366667 3.000000 2.000000 58.333333 0.000000 0.866667 -0.266667 0.000000 0.000000 0.000000 0.000000 4.666667 12.000000 33.258333 20.333333 3.000000 34.625000 34.666667 6.000000 48.000000 41.300000 6.666667 0.333333 3.033333 0.333333 12.233333 302.000000 73.000000 1904.671024 597.184442 38.330073 84.366667 39.180032 80.466667 13.442505 50.300000 0.333333 0.600000 7.000000 6.676949 1.706103 0.329083 7.358874 88.052077 8.321893 1.936060 0.073233 12.539702 2.435745 1.990478 0.825466 0.251375 0.176815 0.000000 57.131288 12.020757 16.761444 22.619711 54.337558 3.223610 3.572207 1.058524 73.703910 0.198840 1.395349 1.681482 2.083333 15.000000 10.333333 1.000000 0.666667 0.333333 0.666667 0.000000 1.333333 0.666667 0.000000 0.000000 0.000000 0.000000 0.000000 15.333333 55.769231 43.181818 32.142857 8.333333 27.906977 30.633333 8.333333 131.000000 26.925000 30.194872 40.625000 18.408045 13.333333 17.987179 0.000000 70.833333 8.333333 19.666667 0.000000 43.000000 532.666667 8.961050 29.345463 43.868450 23.254724 3.223858 91.025962 7.333333 13.666667 52.566667 8.333333 0.333333 302.333333 1531.333333 50.769548 9.595724 2.845528 0.782841 2.597991 2.543108 377.333333 302.000000 79.166667 26.666667 1.000000 0.000000 0.000000 10.666667 10.333333 1.250000 9.666667 8.333333 9.333333 0.000000 0.000000 0.000000 82.333333 15.000000 15.000000 45.933333 NaN 2018.000000 3.000000 2018.000000 4.000000 NaN -1.000000 0.000000 0.000000 -1.000000 0.666667 0.666667 NaN 0.666667 9.666667 3.000000 27.200000 0.060000 0.176667 114.708333 0.000000 0.000000 0.000000 0.933333 0.866667 0.080000 -0.366667 -0.366667 3.000000 2.000000 58.333333 0.000000 0.866667 -0.266667 0.000000 0.000000 0.000000 0.000000 4.666667 12.000000 33.233333 20.333333 3.000000 34.625000 34.666667 6.000000 48.000000 41.300000 6.666667 0.333333 3.033333 0.333333 12.233333 302.000000 73.000000 1904.671024 597.103658 38.327718 84.366667 39.180032 80.466667 13.441365 50.325000 0.333333 0.600000 7.000000 6.676949 1.706103 0.328192 7.358874 88.054636 8.307964 1.935807 0.073300 12.535171 2.435630 1.990167 0.824997 0.250117 0.176815 0.000000 57.140011 12.020757 16.756203 22.619711 54.346396 3.221214 3.573929 1.058127 73.710308 0.198282 1.394568 1.681230 2.083333 15.000000 10.333333 1.000000 0.666667 0.333333 0.666667 0.000000 1.333333 0.666667 0.000000 0.000000 0.000000 0.000000 0.000000 15.333333 55.769231 43.181818 32.142857 8.333333 27.906977 30.633333 8.333333 131.000000 26.933333 30.183981 40.625000 18.408045 13.333333 17.948718 0.000000 70.909091 8.333333 19.666667 0.000000 43.000000 532.916667 8.957279 29.333138 43.868450 23.260019 3.225334 91.027006 7.333333 13.666667 52.566667 8.333333 0.333333 302.333333 1531.583333 50.772488 9.595724 2.845528 0.783429 2.597186 2.543108 377.333333 302.000000 79.166667 26.666667 1.000000 0.000000 0.000000 10.666667 10.333333 1.000000 9.666667 8.333333 9.333333 0.000000 0.000000 0.000000 82.333333 15.000000 15.000000 45.933333 NaN
50% 20.000000 16.000000 NaN 0.000000 1.333333 1.333333 NaN 1.333333 12.000000 4.000000 33.266667 0.096667 0.276667 141.126984 0.333333 0.000000 0.000000 1.233333 1.133333 0.096667 -0.033333 -0.033333 4.000000 2.666667 70.000000 0.333333 1.266667 0.033333 0.000000 0.000000 0.000000 0.000000 6.333333 17.666667 40.133333 23.666667 4.000000 51.233333 41.983333 7.333333 70.883333 53.866667 8.666667 0.666667 6.533333 0.666667 14.200000 369.666667 77.533333 1973.385792 674.276172 40.893394 87.033333 41.918119 84.733333 15.218688 56.616667 1.000000 0.833333 8.666667 7.505258 2.080172 0.499085 8.344460 89.793788 10.206212 2.440634 0.155159 15.109299 2.891967 2.444716 1.030131 0.415153 0.326624 0.052673 64.038769 13.965784 21.682644 27.017143 59.389146 4.180029 4.393993 1.312780 78.137796 0.312337 1.835510 2.419147 2.476006 18.666667 13.000000 1.666667 1.000000 1.000000 1.000000 0.333333 2.000000 1.333333 0.000000 0.000000 0.000000 0.000000 0.000000 17.666667 60.606061 50.000000 37.500000 11.764706 33.333333 36.333333 10.333333 148.666667 29.500000 34.422759 43.166562 21.661238 16.000000 23.076923 0.000000 76.923077 12.333333 24.333333 0.333333 49.333333 598.000000 10.956981 33.231956 46.543912 25.917296 3.799952 92.101589 9.333333 16.333333 58.266667 10.333333 0.666667 365.000000 1888.333333 53.271144 10.804122 3.312019 1.046910 3.311880 3.151388 447.000000 369.666667 82.966667 33.000000 1.666667 0.000000 0.000000 12.333333 12.000000 1.666667 11.666667 12.333333 10.666667 0.000000 0.000000 0.000000 89.666667 18.666667 18.666667 49.866667 NaN 2019.000000 7.000000 2020.000000 5.000000 NaN 0.000000 1.000000 1.000000 0.000000 1.333333 1.333333 NaN 1.333333 12.000000 4.000000 33.266667 0.096667 0.276667 141.096096 0.333333 0.000000 0.000000 1.233333 1.133333 0.096667 -0.033333 -0.033333 4.000000 2.666667 70.000000 0.333333 1.266667 0.033333 0.000000 0.000000 0.000000 0.000000 6.333333 17.500000 40.133333 23.666667 4.000000 51.216667 41.966667 7.333333 70.833333 53.866667 8.666667 0.666667 6.533333 0.666667 14.200000 369.666667 77.533333 1973.299213 674.203472 40.902674 87.033333 41.918119 84.733333 15.216435 56.633333 1.000000 0.833333 8.666667 7.505258 2.080172 0.499002 8.344641 89.807127 10.192873 2.438150 0.155280 15.107914 2.891076 2.442379 1.030131 0.414938 0.326731 0.052673 64.054440 13.965784 21.676691 27.017143 59.397669 4.179519 4.393352 1.312062 78.145767 0.312215 1.833579 2.418674 2.476006 18.666667 13.000000 1.666667 1.000000 1.000000 1.000000 0.333333 2.000000 1.333333 0.000000 0.000000 0.000000 0.000000 0.000000 17.666667 60.606061 50.000000 37.500000 11.764706 33.333333 36.333333 10.333333 148.666667 29.500000 34.416938 43.190925 21.661853 16.000000 23.076923 0.000000 76.923077 12.333333 24.333333 0.333333 49.333333 598.166667 10.955386 33.229361 46.543912 25.917765 3.800716 92.104505 9.333333 16.333333 58.266667 10.333333 0.666667 365.000000 1889.166667 53.272788 10.807099 3.312348 1.047120 3.311526 3.150893 447.000000 369.666667 82.966667 33.000000 1.666667 0.000000 0.000000 12.333333 12.000000 1.666667 11.666667 12.333333 10.666667 0.000000 0.000000 0.000000 89.666667 18.666667 18.666667 49.866667 NaN
75% 29.000000 23.000000 NaN 0.666667 1.666667 2.000000 NaN 1.666667 14.333333 5.000000 39.833333 0.136667 0.400000 174.814815 0.666667 0.333333 0.333333 1.633333 1.500000 0.116667 0.333333 0.333333 5.000000 3.666667 80.600000 0.333333 1.733333 0.300000 0.333333 0.333333 0.000000 0.000000 8.666667 22.333333 48.008333 27.333333 5.000000 66.608333 49.875000 9.000000 88.900000 63.800000 10.666667 1.000000 11.100000 1.000000 16.233333 462.666667 81.866667 2046.497928 761.944411 43.321740 89.300000 44.501404 88.008333 17.192269 63.400000 1.333333 1.133333 10.666667 8.377245 2.488849 0.704380 9.353610 91.678107 11.947923 2.967121 0.259875 18.066159 3.434564 2.904000 1.275412 0.628931 0.495488 0.121175 70.360031 16.085472 27.074844 31.353094 64.326950 5.348022 5.296737 1.594533 82.279813 0.464769 2.369317 3.088833 2.916504 23.000000 17.000000 2.333333 1.666667 1.333333 1.333333 0.666667 3.000000 2.000000 0.333333 0.333333 0.333333 0.333333 0.000000 20.000000 65.724070 56.818182 43.083554 15.733083 39.404609 42.108333 12.333333 168.083333 32.166667 38.637570 45.792658 25.485027 18.000000 29.166667 0.000000 82.012821 15.666667 29.666667 0.333333 56.666667 684.416667 13.116066 37.014643 49.525891 28.669936 4.423012 93.340426 11.333333 19.000000 64.233333 12.333333 1.000000 450.541667 2321.083333 55.817291 12.157871 3.783117 1.351732 4.127864 3.906409 537.666667 462.666667 86.300000 40.666667 2.000000 0.000000 0.000000 14.000000 13.666667 2.333333 14.000000 15.666667 12.333333 0.333333 0.333333 0.000000 97.666667 22.666667 23.000000 54.000000 NaN 2020.000000 11.000000 2021.000000 6.000000 NaN 1.000000 2.000000 2.000000 0.666667 1.666667 2.000000 NaN 1.666667 14.333333 5.000000 39.833333 0.136667 0.400000 174.685847 0.666667 0.333333 0.333333 1.633333 1.500000 0.116667 0.333333 0.333333 5.000000 3.666667 80.600000 0.333333 1.733333 0.300000 0.333333 0.333333 0.000000 0.000000 8.666667 22.333333 48.008333 27.333333 5.000000 66.600000 49.866667 9.000000 88.900000 63.800000 10.666667 1.000000 11.100000 1.000000 16.233333 463.000000 81.875000 2046.262466 761.837938 43.322443 89.300000 44.500754 88.008333 17.189260 63.400000 1.333333 1.133333 10.666667 8.378284 2.488688 0.704225 9.352675 91.692036 11.945364 2.965807 0.259898 18.066159 3.433541 2.902260 1.275691 0.628931 0.496003 0.121230 70.360031 16.080614 27.056263 31.353094 64.338108 5.347347 5.295715 1.594285 82.292768 0.464563 2.369200 3.087634 2.916504 23.000000 17.000000 2.333333 1.666667 1.333333 1.333333 0.666667 3.000000 2.000000 0.333333 0.333333 0.333333 0.333333 0.000000 20.000000 65.714286 56.756757 43.103448 15.733083 39.393939 42.100000 12.333333 168.083333 32.166667 38.637570 45.795794 25.485027 18.000000 29.090909 0.000000 82.051282 15.666667 29.666667 0.333333 56.666667 684.750000 13.116066 37.014643 49.526726 28.669936 4.423812 93.342347 11.333333 19.000000 64.233333 12.333333 1.000000 450.666667 2322.416667 55.825288 12.158055 3.783784 1.351732 4.125392 3.905096 538.000000 463.000000 86.300000 40.666667 2.000000 0.000000 0.000000 14.000000 13.666667 2.333333 14.000000 15.666667 12.333333 0.333333 0.333333 0.000000 97.666667 22.666667 23.000000 54.000000 NaN
max 38.000000 31.000000 NaN 5.333333 5.666667 5.666667 NaN 5.666667 27.666667 11.666667 75.000000 0.500000 1.000000 708.000000 2.333333 1.666667 1.666667 3.833333 3.733333 0.240000 2.400000 2.400000 13.000000 8.000000 100.000000 1.333333 3.933333 1.600000 2.000000 2.000000 1.000000 0.666667 17.666667 42.000000 95.233333 50.333333 10.666667 100.000000 71.666667 18.666667 100.000000 85.850000 21.333333 3.666667 44.766667 3.666667 40.666667 846.333333 91.066667 2398.063380 1296.830986 54.207263 95.100000 52.490660 94.633333 25.879917 83.633333 5.000000 2.833333 21.666667 13.935970 4.793757 2.348066 14.285714 96.042003 21.042831 5.673759 1.083032 30.942092 6.671900 5.632716 2.524698 2.195390 1.541002 0.920680 84.874640 26.916376 47.310513 49.404117 78.316327 11.080836 10.986965 3.247863 91.125642 2.006689 5.189189 6.269113 4.973822 46.333333 38.000000 5.333333 5.666667 5.666667 3.666667 2.333333 10.666667 8.666667 1.333333 2.000000 1.333333 1.666667 1.000000 32.000000 91.666667 79.487179 62.790698 42.857143 71.428571 66.266667 25.333333 268.333333 45.566667 58.685446 56.675063 48.812095 30.666667 54.838710 7.894737 100.000000 31.666667 62.666667 2.666667 78.333333 1024.000000 25.899281 55.932203 63.639323 44.711111 8.444444 96.594982 24.333333 36.333333 87.166667 25.666667 4.666667 746.333333 4209.000000 64.982456 18.909306 6.168549 3.206651 9.473684 9.362280 914.666667 846.333333 94.300000 78.333333 5.000000 1.000000 0.666667 22.333333 22.000000 7.000000 26.666667 31.666667 19.666667 1.666667 2.000000 1.000000 126.666667 50.333333 45.333333 75.766667 NaN 2021.000000 12.000000 2022.000000 6.000000 NaN 9.000000 9.000000 9.000000 5.333333 5.666667 5.666667 NaN 5.666667 27.666667 11.666667 75.000000 0.500000 1.000000 708.000000 2.333333 1.666667 1.666667 3.833333 3.733333 0.240000 2.400000 2.400000 13.000000 8.000000 100.000000 1.333333 3.933333 1.600000 2.000000 2.000000 1.000000 0.666667 17.666667 42.000000 95.233333 50.333333 10.666667 100.000000 71.666667 18.666667 100.000000 85.850000 21.333333 3.666667 44.766667 3.666667 40.666667 846.333333 91.066667 2398.063380 1296.830986 54.207263 95.100000 52.490660 94.633333 25.879917 83.633333 5.000000 2.833333 21.666667 13.935970 4.793757 2.348066 14.285714 96.042003 21.042831 5.673759 1.083032 30.942092 6.671900 5.632716 2.524698 2.195390 1.541002 0.920680 84.874640 26.916376 47.310513 49.404117 78.316327 11.080836 10.986965 3.247863 91.125642 2.006689 5.189189 6.269113 4.973822 46.333333 38.000000 5.333333 5.666667 5.666667 3.666667 2.333333 10.666667 8.666667 1.333333 2.000000 1.333333 1.666667 1.000000 32.000000 91.666667 79.487179 62.790698 42.857143 71.428571 66.266667 25.333333 268.333333 45.566667 58.685446 56.675063 48.812095 30.666667 54.838710 7.894737 100.000000 31.666667 62.666667 2.666667 78.333333 1024.000000 25.899281 55.932203 63.639323 44.711111 8.444444 96.594982 24.333333 36.333333 87.166667 25.666667 4.666667 746.333333 4209.000000 64.982456 18.909306 6.168549 3.206651 9.473684 9.362280 914.666667 846.333333 94.300000 78.333333 5.000000 1.000000 0.666667 22.333333 22.000000 7.000000 26.666667 31.666667 19.666667 1.666667 2.000000 1.000000 126.666667 50.333333 45.333333 75.766667 NaN

Prepare the data

Basically just make numerical data normalised, categorical data encoded and split into train and validation sets

#toggle-hide
def do_pre_proc(dfAll,target = 'NetScore_x'):
    
    dfAll=dfAll.iloc[20:,:]

    if target == 'NetScore_x':
        dfAll=dfAll.drop(columns=['Win_x','opponent_y','team_y','GoalsAgainst_x','GoalsFor_x'])
    elif target=='Win_x':
        dfAll=dfAll.drop(columns=['NetScore_x','opponent_y','team_y','GoalsAgainst_x','GoalsFor_x'])
        dfAll[target]=dfAll[target].map({'W':2,'D':1,'L':0})
    else:
        return 'error'
    
    
    dfAll=dfAll[[c for c in dfAll if c!=target]+[target]]
    
    features_cat=[x for x in dfAll if dfAll[x].dtype=='O']
    features_num = [x for x in dfAll.columns if x != target and dfAll[x].dtype!='O' ]
    
    preprocessor = make_column_transformer(
    (StandardScaler(), features_num),
    (OneHotEncoder(), features_cat),
    )
      
    dfAll=dfAll.fillna(0)
    cond = dfAll.season<2021
    
    predictors = [x for x in dfAll.columns if x != target ]
    X=dfAll.copy()
    
    y=X.pop(target)
    X = preprocessor.fit_transform(X)
    
    
    X_train=X[cond]
    X_valid=X[~cond]
    y_train = y[cond]
    y_valid = y[~cond]

    return X_train, X_valid, y_train, y_valid
X_train, X_valid, y_train, y_valid = do_pre_proc(dfAll,'Win_x')

XGBoost

Gradient Boosting

Gradient boosting is a method that goes through cycles to iteratively add models into an ensemble.

It begins by initializing the ensemble with a single model, whose predictions can be pretty naive. (Even if its predictions are wildly inaccurate, subsequent additions to the ensemble will address those errors.)

Then, we start the cycle:

  • First, we use the current ensemble to generate predictions for each observation in the dataset. To make a prediction, we add the predictions from all models in the ensemble.
  • These predictions are used to calculate a loss function (like mean squared error, for instance).
  • Then, we use the loss function to fit a new model that will be added to the ensemble. Specifically, we determine model parameters so that adding this new model to the ensemble will reduce the loss. (Side note: The “gradient” in “gradient boosting” refers to the fact that we’ll use gradient descent on the loss function to determine the parameters in this new model.)
  • Finally, we add the new model to ensemble, and …
  • … repeat!

GBoost stands for extreme gradient boosting, which is an implementation of gradient boosting with several additional features focused on performance and speed

model_rf = RandomForestClassifier()
model_rf.fit(X_train,y_train)

accuracy_score(y_train,model_rf.predict(X_train)),accuracy_score(y_valid,model_rf.predict(X_valid))
(1.0, 0.49868073878627966)
model_XGB = XGBClassifier()
model_XGB.fit(X_train,y_train)

accuracy_score(y_train,model_XGB.predict(X_train)),accuracy_score(y_valid,model_XGB.predict(X_valid))
(1.0, 0.5092348284960422)

Parameter tuning

n_estimators specifies how many times to go through the modeling cycle described above. It is equal to the number of models that we include in the ensemble.

  • Too low a value causes underfitting, which leads to inaccurate predictions on both training data and test data.
  • Too high a value causes overfitting, which causes accurate predictions on training data, but inaccurate predictions on test data (which is what we care about).

Typical values range from 100-1000

early_stopping_rounds offers a way to automatically find the ideal value for n_estimators. Early stopping causes the model to stop iterating when the validation score stops improving, even if we aren’t at the hard stop for n_estimators. Setting early_stopping_rounds=5 is a reasonable choice. In this case, we stop after 5 straight rounds of deteriorating validation scores.

learning_rate

Instead of getting predictions by simply adding up the predictions from each component model, we can multiply the predictions from each model by a small number (known as the learning rate) before adding them in.

This means each tree we add to the ensemble helps us less. So, we can set a higher value for n_estimators without overfitting. If we use early stopping, the appropriate number of trees will be determined automatically.

In general, a small learning rate and large number of estimators will yield more accurate XGBoost models, though it will also take the model longer to train since it does more iterations through the cycle. As default, XGBoost sets learning_rate=0.1

def do_model(n_estimators,learning_rate):
    model_XGB = XGBClassifier(n_estimators=n_estimators,
             learning_rate=learning_rate,
             early_stopping_rounds=10,
             )
    
    model_XGB.fit(X_train,y_train,
             eval_set=[(X_valid, y_valid)],
             verbose=False)

    acc_train=accuracy_score(y_train,model_XGB.predict(X_train))
    acc_valid=accuracy_score(y_valid,model_XGB.predict(X_valid))
    
    return acc_train, acc_valid

learning_rate=1e-4
n_estimators=[100,250,500,1_000,1500,2_500,5_000,10_000]

score=[]
for n in n_estimators:
    score.append( do_model(n,learning_rate) )
score=np.array(score)
plt.plot(n_estimators,score,'o-')
plt.legend(['train','validation'])
np.max(score[:,1])
0.5290237467018469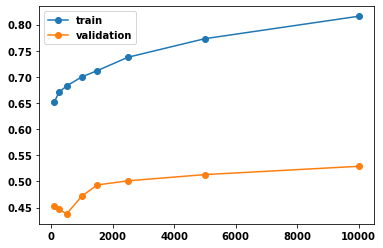

n_estimator=n_estimators[np.argmax(score[:,1])]
model_XGB = XGBClassifier(n_estimators=n_estimator,
             learning_rate=learning_rate,
             early_stopping_rounds=10,
             )
    
model_XGB.fit(X_train,y_train,
         eval_set=[(X_valid, y_valid)],
         verbose=False)

pred_XGB=model_XGB.predict(X_valid)
pred_XGB=[np.argmax(x) for x in pred_XGB ]

Deep Learning

This dataset is prone to lots of overfitting (bias) and also has a high ratio of numberof parameters to number of data points.

To get around the 2 issues: - model has a high dropout rate - a relatively high number of units (i.e. a wide neural network)

For more information see the kaggle notebook of keras binary EPL which goes over this in more detail for the binary issue.

y_valid=pd.get_dummies(y_valid)
y_train=pd.get_dummies(y_train)

drop_pc=0.8
units=512*2
model=keras.Sequential([
        layers.Dense(units,activation='relu',input_shape=[np.shape(X_train)[1]]),
        layers.Dropout(drop_pc),
        layers.Dense(units,activation='relu'),
        layers.Dropout(drop_pc),
        layers.Dense(units,activation='relu'),
        layers.Dropout(drop_pc),
        layers.Dense(3,activation='softmax')
        ])

opt = keras.optimizers.Adam(learning_rate=0.0005)
model.compile(
    optimizer=opt,
    loss='categorical_crossentropy',
    #loss='binary_crossentropy',#for binary classification 0-1
    metrics=['accuracy'],
)
early_stopping = callbacks.EarlyStopping(
    min_delta=0.0001, # minimium amount of change to count as an improvement
    patience=40, # how many epochs to wait before stopping
    restore_best_weights=True,
    monitor='val_accuracy',
)
history = model.fit(
    X_train, y_train,
    validation_data=(X_valid, y_valid),
    batch_size=len(X_valid),
    epochs=700,
    callbacks=[early_stopping],
    verbose=0, # hide the output because we have so many epochs
)
history_df = pd.DataFrame(history.history)

history_df.loc[:, ['loss', 'val_loss']].plot()
history_df.loc[:, ['accuracy', 'val_accuracy']].plot()

print(("Best Validation Loss: {:0.4f}" +\
      "\nBest Validation Accuracy: {:0.4f}")\
      .format(history_df['val_loss'].min(), 
              history_df['val_accuracy'].max()))
Best Validation Loss: 1.0254
Best Validation Accuracy: 0.5369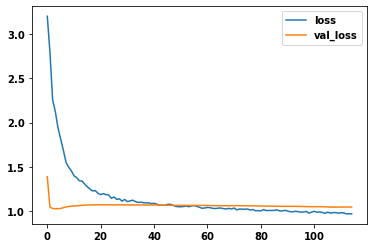

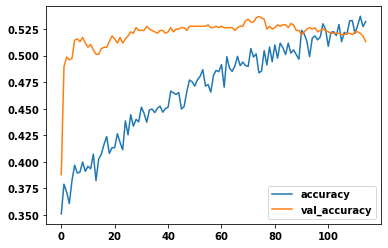
epochs=history_df['val_accuracy'].argmax()
model=keras.Sequential([
        layers.Dense(units,activation='relu',input_shape=[np.shape(X_train)[1]]),
        layers.Dropout(drop_pc),
        layers.Dense(units,activation='relu'),
        layers.Dropout(drop_pc),
        layers.Dense(units,activation='relu'),
        layers.Dropout(drop_pc),
        layers.Dense(3,activation='softmax')
        ])

opt = keras.optimizers.Adam(learning_rate=0.0005)
model.compile(
    optimizer=opt,
    loss='categorical_crossentropy',
    #loss='binary_crossentropy',#for binary classification 0-1
    metrics=['accuracy'],
)
history = model.fit(
    X_train, y_train,
    validation_data=(X_valid, y_valid),
    batch_size=len(X_valid),
    epochs=epochs,
    verbose=0, # hide the output because we have so many epochs
)
preds=model.predict(X_valid).argmax(axis=1)
y_valid_=[np.argmax(y_valid.iloc[i,:]) for i in range(len(y_valid))]
acc_nn=accuracy_score(y_valid_,preds)

print(f"accuracy of nn model = {acc_nn:.3f}")
accuracy of nn model = 0.516

Ensembling

Combine the results of the two models

preds_combo=(model.predict(X_valid)+ model_XGB.predict_proba(X_valid)).argmax(axis=1)

acc_combo=accuracy_score(y_valid_,preds_combo)

print(f"accuracy of combined model = {acc_combo:.3f}")
accuracy of combined model = 0.534